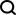Siri Fibonacci dalam C# dalam siri Fibonacci ialah salah satu siri jujukan yang terkenal. Urutannya ialah 0, 1, 1, 2, 3, 5, 8… Siri Fibonacci bermula dari sifar dan satu dan nombor seterusnya ialah hasil tambah dua nombor sebelumnya. Telah dikatakan bahawa Siri Fibonacci dicipta oleh Mr.Leonardo Pisano Bigollo pada abad ke-13. Siri Fibonacci berguna untuk beberapa senario. Pada asasnya ia pada asalnya digunakan untuk menyelesaikan masalah arnab iaitu bilangan arnab yang dilahirkan daripada sepasang. Terdapat juga masalah lain di mana urutan Fibonacci berguna.

Logik Siri Fibonacci

Seperti dalam siri Fibonacci, nombor itu ialah hasil tambah dua nombor sebelumnya. Jadi jika kita mempunyai siri Fibonacci katakan 0, 1, 1, 2, 3, 5, 8, 13, 21… Menurut nombor seterusnya ini ialah jumlah dua sebelumnya seperti 13 dan 21. Jadi nombor seterusnya ialah 13 +21=34.

Berikut ialah logik untuk menjana siri Fibonacci

F(n)= F(n-1) +F(n-2)

Di mana F(n) ialah nombor sebutan dan F(n-1) +F(n-2) ialah jumlah nilai sebelumnya.

Jadi jika kita mempunyai siri 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…

Mengikut logik F(n)= F(n-1) +F(n-2)

F(n)= 55+89

F(n)= 144

Penggal seterusnya ialah 144.

Pelbagai Kaedah mencipta Siri Fibonacci

Siri Fibonacci boleh dijana dalam pelbagai cara.

1. Pendekatan Berulang

Cara ini adalah cara paling mudah untuk menjana siri.

Kod:

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespaceFibonacciDemo
{
classProgram
{
staticint Fibonacci(int n)
{
intfirstnumber = 0, secondnumber = 1, result = 0;
if (n == 0) return 0; //It will return the first number of the series
if (n == 1) return 1; // it will return ?the second number of the series
for (int i = 2; i<= n; i++)? // main processing starts from here
{
result = firstnumber + secondnumber;
firstnumber = secondnumber;
secondnumber = result;
}
return result;
}
staticvoid Main(string[] args)
{
Console.Write("Length of the Fibonacci Series: ");
int length = Convert.ToInt32(Console.ReadLine());
for(int i = 0; i< length; i++)
{
Console.Write("{0} ", Fibonacci(i));
}
Console.ReadKey();
}
}
}

2. Kaedah Rekursif

Ini adalah kaedah lain untuk menyelesaikan masalah ini.

Kaedah 1

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespaceFibonacciDemo
{
classProgram
{
staticint Fibonacci(int n)
{
intfirstnumber = 0, secondnumber = 1, result = 0;
if (n == 0) return 0; //it will return the first number of the series
if (n == 1) return 1; // it will return the second number of the series
return Fibonacci(n-1) + Fibonacci(n-2);
}
staticvoid Main(string[] args)
{
Console.Write("Length of the Fibonacci Series: ");
int length = Convert.ToInt32(Console.ReadLine());
for(int i = 0; i< length; i++)
{
Console.Write("{0} ", Fibonacci(i));
}
Console.ReadKey();
}
}
}

Kaedah 2

using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace FibonacciSeries
{
class Program
{
public static void Fibonacci
(
int firstnumber,
int secondnumber,
int count,
int length,
)
{
if (count <= length)
{
Console.Write("{0} ", firstnumber);
Fibonacci(secondnumber, firstnumber + secondnumber, count + 1, length);
}
}
public static void Main(string[] args)
{
Console.Write("Length of the Fibonacci Series: ");
int length = Convert.ToInt32(Console.ReadLine());
Fibonacci(0, 1, 1, length);
Console.ReadKey();
}
}
}

Output:

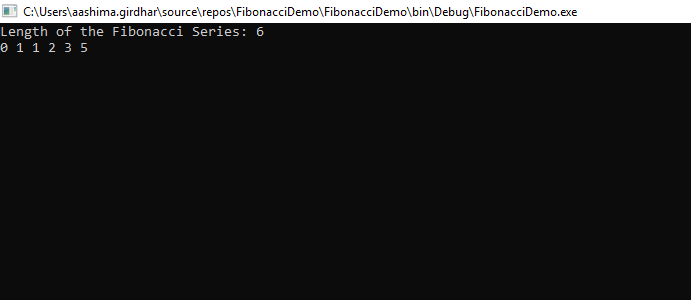
3. Fibonacci dengan menggunakan Array

Kod:

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
public class Program
{
public static int[] Fibonacci(int number)
{
int[] a = new int[number];
a[0] = 0;
a[1] = 1;
for (int i = 2; i < number; i++)
{
a[i] = a[i - 2] + a[i - 1];
}
return a;
}
public static void Main(string[] args)
{
var b = Fibonacci(10);
foreach (var elements in b)
{
Console.WriteLine(elements);
}
}
}

Output:

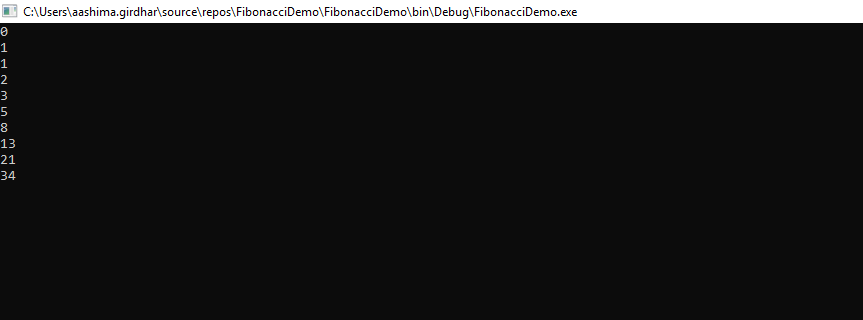
Bagaimana untuk mencari Penggal Kesembilan bagi Siri Fibonacci?

Berikut adalah kaedahnya

Kaedah 1

Kod:

using System;
namespace FibonacciSeries
{
class Program {
public static int NthTerm(int n)
{
if ((n == 0) || (n == 1))
{
return n;
}
else
{
return (NthTerm(n - 1) + NthTerm(n - 2));
}
}
public static void Main(string[] args)
{
Console.Write("Enter the nth term of the Fibonacci Series: ");
int number = Convert.ToInt32(Console.ReadLine());
number = number - 1;
Console.Write(NthTerm(number));
Console.ReadKey();
}
}
}

Kod di atas adalah untuk mencari sebutan ke-n dalam siri Fibonacci. Sebagai contoh, jika kita ingin mencari sebutan ke-12^ke dalam siri itu maka hasilnya ialah 89.

Kaedah 2

(O(Log t) Masa).

Terdapat satu formula ulangan yang lain yang boleh digunakan untuk mencari Nombor Fibonacci ke-T Jika t ialah genap = t/2:

F(t) = [2*F(k-1) + F(k)]*F(k)

Jika t ganjil maka k = (t + 1)/2

F(t) = F(k)*F(k) + F(k-1)*F(k-1)

Matriks Fibonacci

Selepas mendapat penentu, kita akan? mendapat (-1)t = Ft+1Ft-1 – Ft2

FmFt + Fm-1Ft-1 = Fm+t-1

Dengan meletakkan t = t+1,

FmFt+1 + Fm-1Ft = Fm+t

Meletakkan m = t

F2t-1 = Ft2 + Ft-12

F2t = (Ft-1 + Ft+1)Ft = (2Ft-1 + Ft)Ft

Untuk mendapatkan formula kami akan melakukan perkara berikut

Jika t genap, letakkan k = t/2

Jika t ganjil, letakkan k = (t+1)/2

Jadi dengan mengisih nombor ini kita boleh menghalang ruang memori STACK yang sentiasa menggunakan. Ia memberikan kerumitan masa O(n). Algoritma rekursif kurang cekap.

Kod:

int f(n) :
if( n==0 || n==1 )
return n;
else
return f(n-1) + f(n-2)

Sekarang apabila algoritma di atas dijalankan untuk n=4

fn(4)

f(3)????????????? f(2)

f(2)?? f(1)???? f(1)?? f(0)

f(1)? f(0)

Jadi ia adalah pokok. Untuk mengira f(4) kita perlu mengira f(3) dan f(2) dan seterusnya.Untuk nilai kecil 4, f(2) dikira dua kali dan f(1) dikira tiga kali. Bilangan penambahan ini akan meningkat untuk jumlah yang besar.

Terdapat andaian bahawa bilangan penambahan yang diperlukan untuk mengira f (n) ialah f (n+1) -1.

Kesimpulan

Di sini kaedah lelaran sentiasa diutamakan kerana ia mempunyai pendekatan yang lebih pantas untuk menyelesaikan masalah seperti ini. Di sini kami menyimpan nombor pertama dan kedua siri Fibonacci dalam nombor sebelumnya dan nombor sebelumnya (ini adalah dua pembolehubah) dan juga kami menggunakan nombor semasa untuk menyimpan nombor Fibonacci.

Atas ialah kandungan terperinci Siri Fibonacci dalam C#. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!